順伝播型ネットワークの項目における全結合ニューラルネットワークについて解説します。
目次
ニューラルネットワークとは
ニューラルネットワーク(NN)とは、「ニューロン」をたくさん組み合わせたものです。
NNのうち、一方通行のものをFeed-Forward NNという。
4層以上の多層NNをDeep Learning(DNN)という。
活性化関数がないとただの線形モデルになってしまう。
線形モデルを組み合わせても線形であることは変わらないので、多層にする意味が薄れてしまう。
活性化関数を通してモデルに非線形性を与えるコトで、より複雑で自由度の高いモデルを作ることができる。ただし、学習は難しくなる。
活性化関数
以下に、それぞれの活性化関数の数式を示します:
シグモイド関数 (Sigmoid Function):
\(\sigma(x) = \frac{1}{1 + e^{-x}}\)
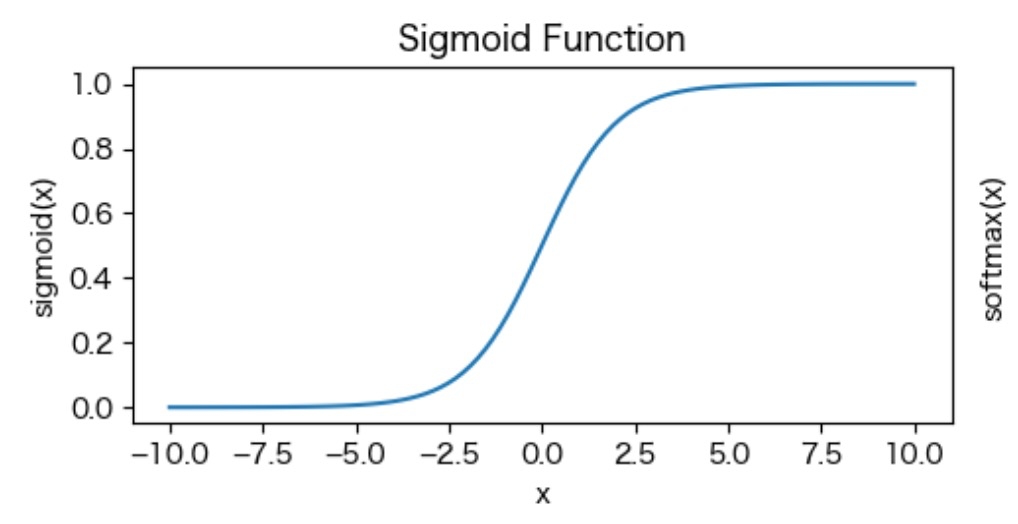
x=0のときにy=0.5を通る
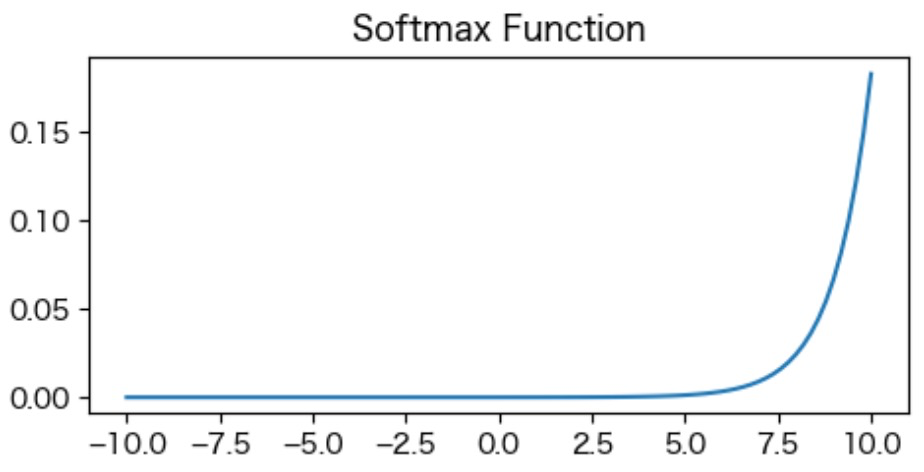
SoftMax関数 (Softmax Function):
\(\text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^N e^{x_j}}\)
ここで、\(x_i\)は入力ベクトル\(x\)の要素であり、\(N\)はベクトル\(x\)の次元数です。
ReLU関数 (Rectified Linear Unit Function):
\(\text{ReLU}(x) = \max(0, x)\)Leaky ReLU関数 (Leaky Rectified Linear Unit Function):
\(\text{Leaky ReLU}(x) = \begin{cases}x, & \text{if } x \geq 0 \\alpha x, & \text{otherwise}\end{cases}\)
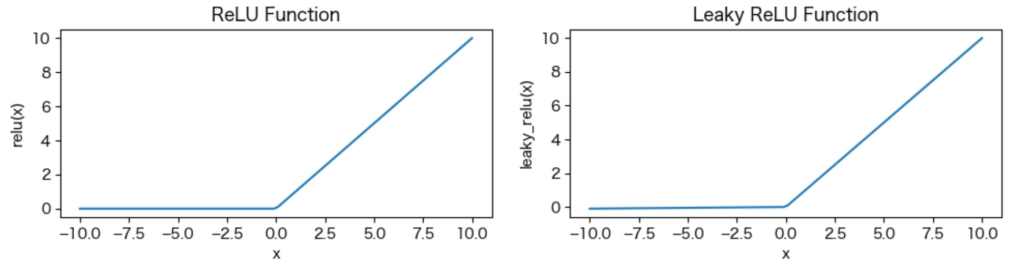
ReLuはx=0から一時関数的に値が上る。Leaky ReLuはx=0までに若干、値が上がる
ReLU関数の特徴と利点:
- 非線形性: ReLU関数は非線形な活性化関数であり、ニューラルネットワークの層の間で非線形性を導入するのに役立ちます。これにより、ネットワークがより複雑な関数を学習できるようになります。
- 計算効率: ReLU関数は計算上非常に効率的であり、指数関数などの複雑な演算が不要です。
- スパース性: 入力が負の値の場合、ReLU関数は0を出力します。これにより、ネットワークがスパース性を持ち、一部のニューロンが非アクティブになることがあります。これは過学習を防ぐ効果があるとされています。
ReLU関数はディープラーニングの活性化関数として広く使われていますが、一方で注意点もあります:
- 死んだニューロン問題: 一部のニューロンが学習の過程で0になり、その後ずっと0を出力し続ける場合があります。これを「死んだニューロン問題」と呼び、学習が進行しなくなる可能性があります。これを回避するために、Leaky ReLUなどの改良されたReLU関数が使われることもあります。
- 勾配消失問題: ReLU関数は入力が負の値の場合に勾配が0になります。したがって、逆伝搬の際に勾配が消失してしまう可能性があります。これは、非常に深いネットワークにおいて学習が進まなくなる問題として知られています。
ReLU関数はディープラーニングの基本的なアーキテクチャで広く使われており、そのシンプルな形式と効率性から、多くの場合に優れたパフォーマンスを発揮します。ただし、ディープネットワークの設計や学習において、ReLU関数の特性に注意しながら適切に使用する必要があります。
ここで、\(\alpha\)は漏れた\(leaky\)範囲での傾斜を示す小さな定数です。
tanh関数 (Hyperbolic Tangent Function):
\(\tanh(x) = \frac{e^x – e^{-x}}{e^x + e^{-x}}\)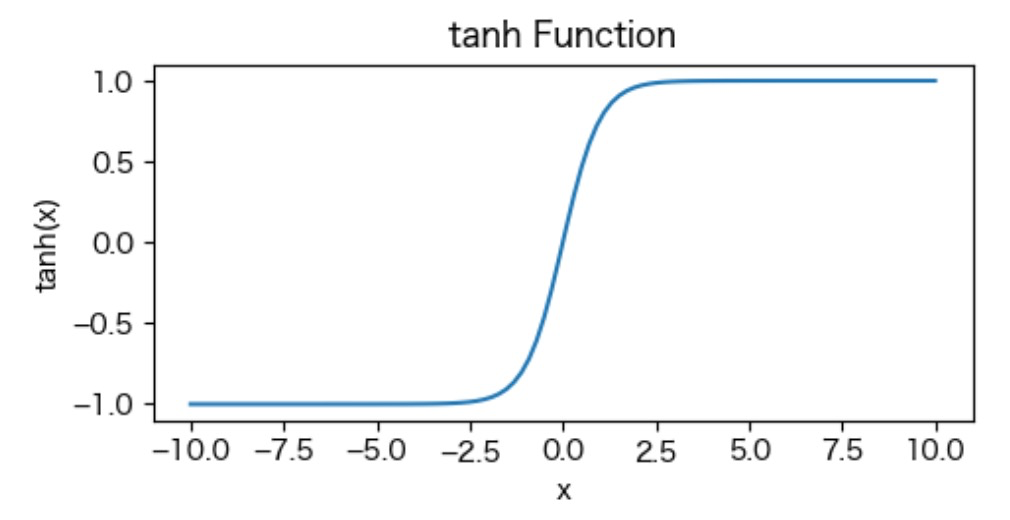
シグモイド関数の2倍みたいな感じ。
x=0のときにy=0を通る
コスト関数(損失関数)
何かの基準で「悪さ」を決めて、悪さが少なくなるようなパラメータを学習する。
この基準をコスト関数という。
損失関数(Loss Function)は、機械学習やディープラーニングのタスクにおいて、モデルの性能を評価するための関数です。モデルが出力する予測と、真の目標値(またはラベル)との差を表現します。損失関数の値が小さいほど、モデルの予測が真の値に近いことを意味します。
損失関数の主な役割は、以下の2つです:
- モデルの性能評価: 損失関数はモデルの出力と真の値との誤差を表現するため、モデルの性能を評価する指標として利用されます。訓練中にこの値を最小化することが目標となります。
- 学習: 損失関数を最小化するようなパラメータ(重みやバイアスなど)を見つけることによって、モデルを学習させるのに使用されます。訓練データを使って損失関数を最小化するようにモデルのパラメータを調整していくことで、モデルがデータのパターンを学習し、予測性能が向上します。
一般的な損失関数としては、以下のようなものがあります:
- 平均二乗誤差(Mean Squared Error, MSE): 回帰タスクでよく使われる損失関数で、予測値と真の値の差の二乗の平均を計算します。
- 交差エントロピー誤差(Cross-Entropy Error, CEE)またはロジスティック損失: 分類タスクでよく使われる損失関数で、クラスの確率分布の差を表現します。二値分類の場合は「バイナリクロスエントロピー誤差」、多クラス分類の場合は「カテゴリクロスエントロピー誤差」と呼ばれることもあります。
- ヒンジ損失(Hinge Loss): サポートベクターマシンなどのSVM(Support Vector Machine)で使われる損失関数で、分類のマージンを考慮しています。
- KLダイバージェンス(Kullback-Leibler Divergence, KL Divergence): 確率分布の差を測る指標で、生成モデルなどで使われることがあります。
損失関数は、特定のタスクやモデルに合わせて適切に選択する必要があります。適切な損失関数を選ぶことで、モデルの学習が効率的に進み、望む性能を得ることができます。
ニューラルネットワークの最適化
最適化アプローチ
- 正解の値とNNが出した値を比べる
- どのくらい間違っているのか(損失)を求める
- 間違いが少なくなるように少しだけWを増減させる
クロスエントロピー Cross Entropy
分類問題の際によく使われる。
最尤推定から導くことができる。
確率pで1だと推定しているとき、実際には確率qで1だったと判明した時にどれくらい予想が待ちがているか、のずれ具合を見ている
勾配降下法
今いる場所がどっちにどれくらい傾いているかがわかれば、そちらの方に少し移動すれば少し改善される。それを繰り返して損失の少ない良い場所が求められるはず。
勾配降下法の問題点
単純に1個ずつ勾配を求めようとすると途方もない時間がかかる
最寄りの低いところにいけたとして、全体で見た時に一番低いかどうかがわからない
誤差逆伝播法
確率的勾配降下法
