深層ニューラルネットワークにおいて、誤差逆伝播法(Backpropagation)は、
ネットワークの重みとバイアスを更新するために使用されるアルゴリズムです。
このアルゴリズムは、出力の予測値と実際の目標値との誤差を計算し、それを各層に逆方向に伝播させながら、各パラメータの勾配を求める手法です。
以下に、誤差逆伝播法の基本的なステップを説明します。
- フォワードパス(順伝播): 入力データをネットワークに与え、各層のユニットの出力を計算します。フォワードパス中では、入力から出力までの活性化関数や重みに基づく計算が行われます。
- 誤差計算: フォワードパスを通じて得られたネットワークの出力と実際の目標値との誤差を計算します。一般的に、平均二乗誤差(Mean Squared Error)などの損失関数を使用して誤差を評価します。
- バックワードパス(逆伝播): 誤差を出力層から始めて、各層に逆方向に伝播させます。逆伝播中では、各層のパラメータに対する誤差の影響を計算するために連鎖律(Chain Rule)が利用されます。
- 勾配計算: 各層のユニットの出力と誤差を元に、勾配(パラメータに対する損失の微分)を計算します。これにより、各パラメータが損失関数をどれだけ変化させるかを示す情報が得られます。
- パラメータ更新: 計算された勾配を使って、勾配降下法などの最適化アルゴリズムを適用して、ネットワークの重みとバイアスを更新します。これにより、ネットワークの予測が実際のデータに適合するように調整されます。

ここで、
\(x\) は入力、
\(y\) は目標値、
\(\hat{y}\) は予測値、
\(W^{(i)}\) と
\(b^{(i)}\) は各層の重みとバイアス、
\(\delta^{(i)}\) は誤差項、
\(\alpha\) は学習率、
\(\odot\) は要素ごとの積を示します。
連鎖律(Chain Rule)は、複数の関数の合成の微分を求める際に使用される微分法則です。
関数が他の関数の中に含まれる場合、その合成関数の微分は、それぞれの関数の微分の積として表現されます。連鎖律は、多変数関数の微分を効果的に計算するための基本的なテクニックであり、深層ニューラルネットワークにおいて勾配の逆伝播を行う際にも重要な役割を果たしています。
数学的には、連鎖律は以下のように表現されます。
2つの関数 \(f\) と \(g\) があるとします。
それぞれの関数の微分は \(f’\) と \(g’\) とします。
このとき、合成関数 \((f \circ g)(x) = f(g(x))\) の微分は次のように表されます:
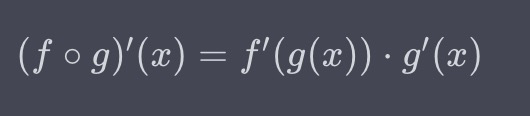
この式が連鎖律です。連鎖律によって、合成関数の微分をそれぞれの関数の微分の積として計算することができます。
例として、関数 \(h(x) = f(g(x))\) の微分を考えてみましょう。
この場合、\(h'(x)\) を求めるために連鎖律を使用します。
\(h(x)\) の微分は次のように計算されます:
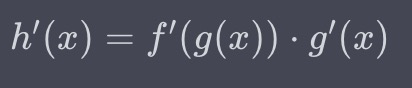
このようにして、連鎖律を利用して、複雑な合成関数の微分を簡単に計算することができます。
連鎖律は、ニューラルネットワークのバックプロパゲーションにおいて、各層の微分を連鎖的に計算するために使用され、勾配の逆伝播を効率的に行う際に重要な役割を果たしています。
