目次
サンプリング
音声データ処理における「サンプリング」とは、アナログ音声をデジタルデータとして扱う際に行われる重要なステップの一つです。アナログ音声は連続的な波形で表現されますが、デジタルデータとして扱うためには一定の間隔で音声の値を取得し、その値をデジタル化します。これがサンプリングです。
サンプリングの手順は以下のようになります:
- サンプリングレートの決定:
サンプリングレートは、1秒あたりに取得する音声サンプルの数を表します。例えば、44.1kHzのサンプリングレートは、1秒間に44,100個のサンプルを取得することを意味します。一般的な音声処理アプリケーションでは、44.1kHzや48kHzがよく使われます。 - アナログ音声のサンプリング:
実際の音声波形から、サンプリングレートに応じた間隔で音声の値をサンプルとして取得します。この際、連続的な波形を離散的な値に変換するために、アナログ-デジタル変換器(ADC)が用いられます。 - デジタル音声データの生成:
サンプルとして取得した音声の値をデジタルデータとして扱い、音声ファイルなどに保存することで、デジタル音声データが生成されます。
サンプリングによって得られたデジタルデータは、連続的な波形の近似として表現されます。サンプリングレートが高いほど、元の音声波形に近い再現が可能ですが、同時にファイルサイズも増大します。
しかし、低いサンプリングレートを使用すると音質が劣化する可能性があるため、一般的な音声データ処理では高いサンプリングレートが選択されることが多いです。ただし、特定のアプリケーションや再生環境においては、適切なバランスを見つける必要があります。
短時間フーリエ変換(STFT)
短時間フーリエ変換(Short-Time Fourier Transform、STFT)は、音声データ分析や信号処理において非常に重要な手法の一つです。STFTは、時間的に変動する信号の周波数特性を解析するために使用されます。
通常のフーリエ変換は、全ての信号データを一度に周波数領域に変換しますが、STFTは信号を小さな時間窓(ウィンドウ)に区切り、それぞれの時間窓に対してフーリエ変換を行います。この時間窓は、一般的にハミング窓やハンニング窓などの窓関数が使われます。
STFTによる音声データの解析手順は以下のようになります:
- 時間窓の設定:
解析したい音声データを小さな時間窓に分割します。窓のサイズは、解析したい周波数分解能と時間分解能のトレードオフによって選択されます。窓のサイズが小さいほど、時間の詳細な変化を捉えることができますが、周波数分解能は低くなります。逆に、窓のサイズが大きいほど、周波数分解能は高くなりますが、時間の詳細な変化を捉えることが難しくなります。 - 窓関数の適用:
各時間窓に対して、選択した窓関数を掛けることで、信号が窓に収められます。窓関数は、窓の端で生じる周波数スペクトルの漏れを抑えるために使用されます。 - フーリエ変換の実行:
窓関数を掛けた信号に対して、フーリエ変換を行います。これにより、各時間窓の周波数成分が得られます。 - スペクトログラムの生成:
各時間窓に対して得られた周波数成分を連結してスペクトログラムと呼ばれる行列を生成します。スペクトログラムは、時間を横軸、周波数を縦軸とする2次元のグラフで、信号の時間的な周波数特性を視覚的に表現するのに使われます。
STFTを用いることで、音声データの周波数特性が時間的にどのように変化するかを分析できます。音声分析においては、STFTを用いたスペクトログラムを視覚化し、音のスペクトル変化や瞬間的な特徴を把握することが有用です。また、音声処理の他にも、画像処理やさまざまな信号処理アプリケーションでもSTFTが活用されています。
Sure! STFTの数式をLaTeX形式で表現すると以下のようになります:
STFTは、信号\(x(t)\)に対して時間窓\(w(t)\)を用いてフーリエ変換を行う操作です。時間窓(w(t))の中心を時刻(t)とした場合のSTFTは次のように表されます:
\(X(\omega, t) = \int_{-\infty}^{\infty} x(\tau) \cdot w(\tau – t) \cdot e^{-j\omega\tau} d\tau\)ここで、\(X(\omega, t)\)は周波数\(\omega\)と時刻(t)におけるSTFT結果を表します。
\(x(\tau)\)は入力信号の波形、\(w(\tau – t)\)は時間窓関数、\(e^{-j\omega\tau}\)は複素正弦波(フーリエ変換の核)を表します。この積分は、信号\(x(t)\)を時間窓\(w(t)\)で重み付けし、周波数領域に変換しています。STFTはこの操作を異なる時間刻み幅(t)に対して行うことで、時間的な変化を捉えることができます。
Pythonでの実装例
import librosa
import librosa.display
import matplotlib.pyplot as plt
import numpy as np
def plot_waveform_and_spectrogram(waveform, sample_rate, n_fft=2048, hop_length=512):
# 波形のグラフ表示
plt.figure(figsize=(10, 6))
librosa.display.waveshow(waveform, sr=sample_rate)
plt.title("Waveform")
plt.xlabel("Time (seconds)")
plt.ylabel("Amplitude")
plt.show()
# STFTの計算
spectrogram = librosa.stft(waveform, n_fft=n_fft, hop_length=hop_length)
# STFTのグラフ表示
plt.figure(figsize=(10, 6))
librosa.display.specshow(librosa.amplitude_to_db(spectrogram, ref=np.max),
y_axis='log', x_axis='time', sr=sample_rate, hop_length=hop_length)
plt.colorbar(format='%+2.0f dB')
plt.title("Spectrogram")
plt.xlabel("Time (seconds)")
plt.ylabel("Frequency (Hz)")
plt.show()
# wavファイルの読み込み
file_path = "path/to/your/wav/file.wav"
waveform, sample_rate = librosa.load(file_path, sr=None)
# 波形とスペクトログラムのグラフ表示
plot_waveform_and_spectrogram(waveform, sample_rate)
データファイルは、音声で「おはようございます」と発声しているものを使用。
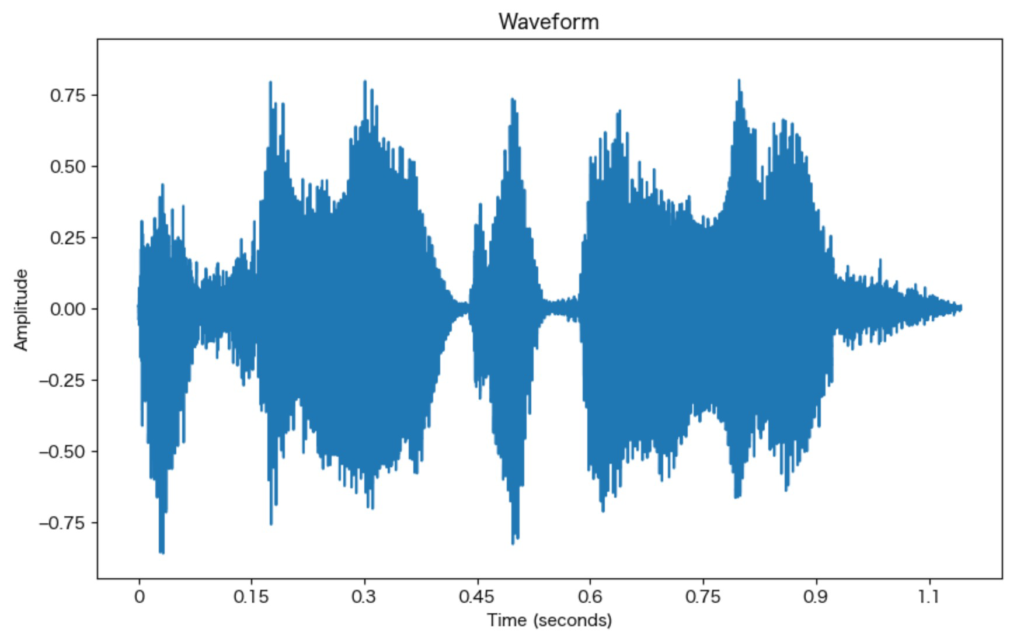
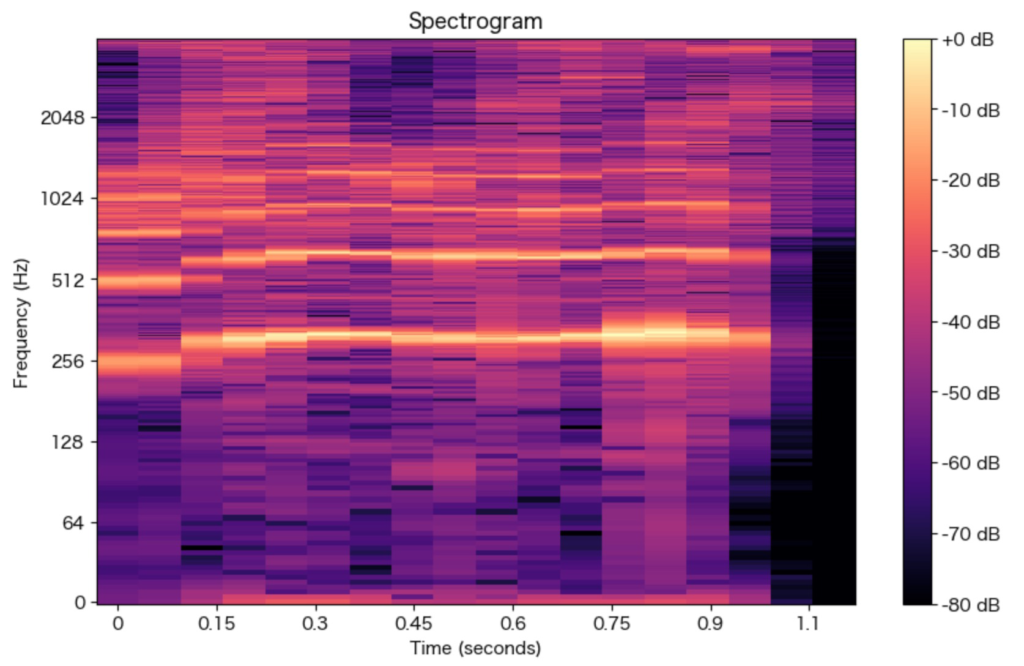
ちなみにlibrosaを使わずに
numpyでの実装は以下の通り。
import numpy as np
import scipy.signal
import matplotlib.pyplot as plt
import wave
def stft(signal, window_size, hop_size):
# ハミング窓を作成
window = np.hamming(window_size)
# STFTの計算
frames = len(signal) // hop_size + 1
stft_matrix = np.zeros((window_size, frames), dtype=np.complex128)
for i in range(frames):
start = i * hop_size
end = min(start + window_size, len(signal))
frame = np.zeros(window_size)
frame[:end-start] = signal[start:end]
stft_matrix[:, i] = np.fft.fft(frame * window, window_size)
return stft_matrix
def plot_waveform_and_spectrogram(waveform, sample_rate, n_fft=2048, hop_length=512):
# 波形のグラフ表示
plt.figure(figsize=(10, 6))
plt.plot(np.arange(len(waveform)) / sample_rate, waveform)
plt.title("Waveform")
plt.xlabel("Time (seconds)")
plt.ylabel("Amplitude")
plt.show()
# STFTの計算
spectrogram = stft(waveform, n_fft, hop_length)
# STFTのグラフ表示
plt.figure(figsize=(10, 6))
plt.imshow(np.abs(spectrogram), aspect='auto', origin='lower', cmap='inferno', extent=[0, len(waveform) / sample_rate, 0, sample_rate / 2])
plt.colorbar(format='%+2.0f dB')
plt.title("Spectrogram")
plt.xlabel("Time (seconds)")
plt.ylabel("Frequency (Hz)")
plt.show()
# wavファイルの読み込み
file_path = "path/to/your/wav/file.wav"
with wave.open(file_path, 'rb') as wf:
sample_rate = wf.getframerate()
waveform = np.frombuffer(wf.readframes(wf.getnframes()), dtype=np.int16)
# 波形とスペクトログラムのグラフ表示
plot_waveform_and_spectrogram(waveform, sample_rate)
librosa.stftを使った場合とNumPyを使って独自に実装した場合、計算方法やパラメータの扱いに差異があるため、結果が異なるのは正常です。
メル尺度
メル尺度(Mel scale)は、人間の聴覚特性に基づいて設計された周波数尺度です。一般的な線形の周波数尺度(ヘルツ)では、人間の聴覚特性を反映するのに適していないため、音声分析や音響工学などの領域でよく使用されます。
メル尺度は、低い周波数領域では高い解像度を持ち、高い周波数領域では低い解像度を持つように設計されています。これにより、人間の聴覚特性に合った音の知覚を模倣することができます。
一般的に、周波数(f)をメル尺度に変換する公式は以下のように表されます:
\(m = 2595 \cdot \log_{10}\left(1 + \frac{f}{700}\right)\)ここで、(m)は変換後のメル尺度の値を表します。
また、逆にメル尺度(m)を周波数(f)に変換する公式は以下のようになります:
\(f = 700 \cdot \left(10^{\frac{m}{2595}} – 1\right)\)メル尺度は主に以下のような用途に使われます:
- メルフィルタバンク:
メル尺度を使用して設計されたメルフィルタバンクは、音声分析や音声特徴抽出に広く使用されます。メルフィルタバンクは、周波数スペクトルを一定のバンドに分割し、各バンドのエネルギーを計算するのに使われます。 - メルケプストラム係数(MFCC):
MFCCは音声認識などの音声処理タスクで特徴抽出に使用される手法です。MFCCはメル尺度を使用して周波数スペクトルを圧縮し、音声の重要な特徴を抽出します。 - 音高変換:
メル尺度は周波数スペクトルを人間の聴覚に対応する尺度に変換するのに使用され、音声や楽器の音高変換に利用されることがあります。
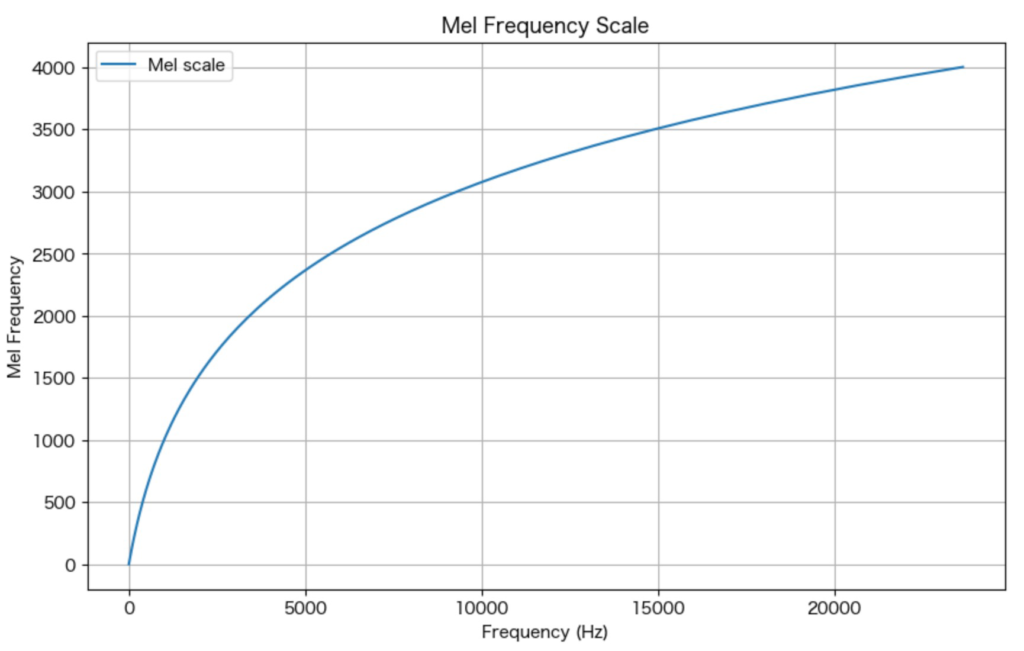
メル尺度は、音声処理において人間の聴覚特性を考慮する際に重要なツールとなっており、特に音声認識や音声合成、音楽情報検索などの分野で幅広く利用されています。
pythonでの実装例
import librosa
import librosa.display
import matplotlib.pyplot as plt
# wavファイルの読み込み
file_path = "./ohayou.wav"
waveform, sample_rate = librosa.load(file_path, sr=None)
# STFTの計算
spectrogram = librosa.stft(waveform, n_fft=2048, hop_length=512)
# メル周波数の計算
mel_frequencies = librosa.mel_frequencies(n_mels=128, fmin=0, fmax=sample_rate/2)
# メル周波数に対応するインデックスを計算
mel_freq_index = librosa.mel_to_hz(mel_frequencies, htk=True)
# スペクトログラムの表示
plt.figure(figsize=(12, 6))
# STFT結果の表示
plt.subplot(1, 2, 1)
librosa.display.specshow(librosa.amplitude_to_db(spectrogram, ref=np.max),
y_axis='log', x_axis='time', sr=sample_rate, hop_length=512)
plt.colorbar(format='%+2.0f dB')
plt.title("STFT Spectrogram")
plt.xlabel("Time (seconds)")
plt.ylabel("Frequency (Hz)")
# メル周波数に変換した結果の表示
mel_spectrogram = librosa.feature.melspectrogram(S=librosa.amplitude_to_db(spectrogram, ref=np.max)**2, sr=sample_rate)
plt.subplot(1, 2, 2)
librosa.display.specshow(librosa.amplitude_to_db(mel_spectrogram, ref=np.max),
y_axis='log', x_axis='time', sr=sample_rate, hop_length=512)
plt.colorbar(format='%+2.0f dB')
plt.title("Mel Spectrogram")
plt.xlabel("Time (seconds)")
plt.ylabel("Mel Frequency")
plt.tight_layout()
plt.show()
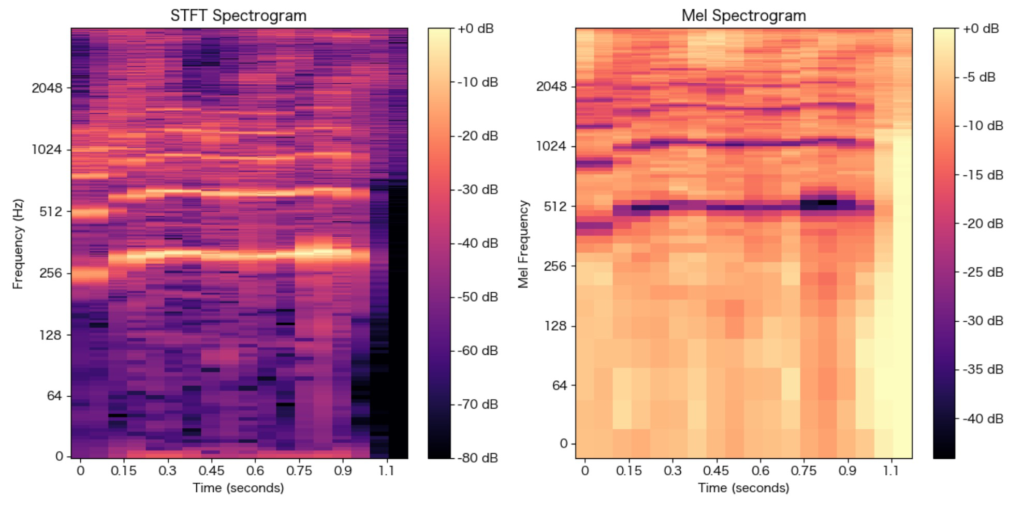
メル尺度では、周波数が高くなるにつれてメル周波数も対数的に増加します。これにより、低周波数帯域では解像度が高く、高周波数帯域では解像度が低くなります。メル周波数スケールのプロットによって、この特性を確認することができます。スペクトログラムにおいては、対数スケールを用いて表示することで、人間の聴覚特性に近い視覚的表現を得ることができます。
CTC(Connectionist Temporal Classification)
出力ラベルが不完全な場合に使われる手法。
CTC(Connectionist Temporal Classification)は、音声認識や文字認識などの系列データに対する学習と推論を行う際に使われる重要な手法の一つです。特に、入力と出力の長さが異なる場合や、出力のラベルが不完全な場合に有用です。
CTCは、アレクサンダー・グレーヴェス(Alex Graves)によって提案された手法で、リカレントニューラルネットワーク(RNN)をベースとしています。CTCは、以下のようなケースで役立ちます:
- 可変長シーケンスのマッピング:
CTCは、入力と出力のシーケンスが長さが異なる場合に有効です。音声認識などでは、音声データとテキストデータの対応付けが複雑で、一対一の対応が得られない場合があります。CTCは、このような問題を解決するのに適しています。 - ラベル不完全なデータ:
CTCは、データセットにラベルの付いていない部分がある場合でも学習が可能です。CTCは、各出力に対して「ラベルなし」の特別なトークンを導入することで、ラベル不完全なデータをうまく扱うことができます。
CTCの動作原理は、与えられた入力シーケンスから出力シーケンスを推定するとき、各時間ステップにおけるラベルの対応関係を学習することにあります。CTCでは、入力と出力の長さの差をカバーするため、一般的にブランクトークン(ラベルなし)が使用されます。
CTCの学習は、通常、逐次的なアルゴリズム(ビタビアルゴリズムなど)を用いて、最適な出力シーケンスを見つけることを目指します。RNNやその派生モデル(LSTMやGRUなど)がCTCによく利用されるモデルアーキテクチャです。
CTCは音声認識、文字認識、言語モデリングなどの様々なタスクで広く応用されており、シーケンスデータに対する柔軟な学習と推論を実現するための有力な手法として活用されています。
CTC(Connectionist Temporal Classification)は、音声認識や文字認識などの系列データに対する学習と推論を行う際に使われる重要な手法の一つです。特に、入力と出力の長さが異なる場合や、出力のラベルが不完全な場合に有用です。
CTCは、アレクサンダー・グレーヴェス(Alex Graves)によって提案された手法で、リカレントニューラルネットワーク(RNN)をベースとしています。CTCは、以下のようなケースで役立ちます:
- 可変長シーケンスのマッピング:
CTCは、入力と出力のシーケンスが長さが異なる場合に有効です。音声認識などでは、音声データとテキストデータの対応付けが複雑で、一対一の対応が得られない場合があります。CTCは、このような問題を解決するのに適しています。 - ラベル不完全なデータ:
CTCは、データセットにラベルの付いていない部分がある場合でも学習が可能です。CTCは、各出力に対して「ラベルなし」の特別なトークンを導入することで、ラベル不完全なデータをうまく扱うことができます。
CTCの動作原理は、与えられた入力シーケンスから出力シーケンスを推定するとき、各時間ステップにおけるラベルの対応関係を学習することにあります。CTCでは、入力と出力の長さの差をカバーするため、一般的にブランクトークン(ラベルなし)が使用されます。
CTCの学習は、通常、逐次的なアルゴリズム(ビタビアルゴリズムなど)を用いて、最適な出力シーケンスを見つけることを目指します。RNNやその派生モデル(LSTMやGRUなど)がCTCによく利用されるモデルアーキテクチャです。
CTCは音声認識、文字認識、言語モデリングなどの様々なタスクで広く応用されており、シーケンスデータに対する柔軟な学習と推論を実現するための有力な手法として活用されています。
pytorchを使った実装例
import torch
import torchaudio
import torch.nn as nn
import torch.optim as optim
# wavファイルのパス
file_path = "./ohayou.wav"
# wavファイルをTensorに変換
waveform, sample_rate = torchaudio.load(file_path)
# ラベルデータ(ここではダミーデータを使用)
labels = torch.tensor([1, 2, 1])
# モデルの定義
class CTCModel(nn.Module):
def __init__(self, num_classes):
super(CTCModel, self).__init__()
self.conv1 = nn.Conv1d(in_channels=waveform.size(0), out_channels=64, kernel_size=3, stride=1, padding=1)
self.relu = nn.ReLU()
self.dropout = nn.Dropout(0.2)
self.lstm = nn.LSTM(64, 128, batch_first=True, bidirectional=True)
self.fc = nn.Linear(256, num_classes)
def forward(self, x):
x = self.conv1(x)
x = self.relu(x)
x = self.dropout(x)
x, _ = self.lstm(x)
x = self.fc(x)
return x
# モデルのインスタンス化
model = CTCModel(num_classes=3)
# 損失関数
loss_fn = nn.CTCLoss()
# オプティマイザー
optimizer = optim.Adam(model.parameters(), lr=0.001)
# トレーニングループ(ダミーデータを使った例)
num_epochs = 50
for epoch in range(num_epochs):
optimizer.zero_grad()
outputs = model(waveform.unsqueeze(0))
outputs = outputs.permute(2, 0, 1)
input_lengths = torch.tensor([outputs.size(0)])
target_lengths = torch.tensor([len(labels)])
loss = loss_fn(outputs, labels.unsqueeze(0), input_lengths, target_lengths)
loss.backward()
optimizer.step()
print(f"Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}")
# 推論
with torch.no_grad():
outputs = model(waveform.unsqueeze(0))
outputs = outputs.permute(2, 0, 1)
_, output_lengths = torch.max(outputs, dim=2)
output_lengths = output_lengths.squeeze(0)
print("Predicted Label:", output_lengths.tolist())
もちろん、プログラムの解説をいたします。
このプログラムは、PyTorchを使用してCTC(Connectionist Temporal Classification)モデルを定義し、ダミーデータを使ってトレーニングと推論を行う例です。CTCモデルは音声認識や文字認識などの系列データを扱う際に使用される手法の一つで、入力と出力の長さが異なる場合やラベル不完全なデータにも対応できます。
プログラムの構造を以下に解説します:
- ライブラリのインポート:
必要なPyTorch関連のライブラリ(torch, torchaudio, nn, optim)をインポートします。 - wavファイルの読み込み:
torchaudio.load関数を使用して、指定されたwavファイル(./ohayou.wav)を読み込みます。waveformに音声データが、sample_rateにサンプリングレートが格納されます。 - ダミーラベルの設定:
labelsとして、ダミーデータ[1, 2, 1]を設定します。実際のタスクでは音声データに対応するテキストラベルが用意されますが、この例では単純化のためにダミーデータを使います。 - CTCモデルの定義:
CTCModelというクラスを定義します。このモデルは1次元の畳み込み層、ReLU活性化関数、ドロップアウト、双方向LSTM層、全結合層から構成されています。このモデルは音声データを入力とし、CTCによる出力を行います。 - 損失関数とオプティマイザーの設定:
CTCの損失関数CTCLossをloss_fnとして定義します。また、オプティマイザーとしてAdamを使用し、optimizerとして設定します。 - トレーニングループ:
num_epochs回数だけトレーニングループを回します。1エポックごとに、以下の手順を実行します。
- オプティマイザーの勾配を0にリセット(
optimizer.zero_grad()) - モデルに音声データを入力として与えて出力を計算
- CTCの損失を計算(
loss_fnを用いて目標ラベルlabelsと出力outputsの間の損失を計算) - 勾配を計算し、モデルを更新(
loss.backward()とoptimizer.step()) - 各エポックごとに損失を表示
- 推論:
モデルを使用して音声データに対して推論を行います。with torch.no_grad()を使用して計算グラフを無効化し、勾配の計算をスキップします。モデルに音声データを入力として与えて出力を計算し、それを整形して最終的な推論結果を表示します。
以上が、このプログラムの概要となります。実際のタスクに合わせて音声データとテキストラベルを適切に用意し、モデルのアーキテクチャやハイパーパラメータを調整することで、音声認識や文字認識などのタスクを解決することができます。
